こんにちは!マシューのD&D部屋です。
今回は集合論の第7回目ということで、写像について紹介します。
ざっくりとしたイメージは関数のようなものと捉えると良いと思います。
写像とは
2つの集合A,Bをまず考えます(A=Bでも,A≠Bでも大丈夫です)。
そしてAの任意の元を入力したしたときにBのある元が1つ出力されるようなものを写像と言います。
記号は(1)のように表します(この場合fが写像)。
f:A→B・・・(1)
特にAの元aをf(a)に送ることを(2)のように表します。
f:A→B,a↦f(a)・・・(2)
ここで集合同士の矢印(→)と集合の元同士の矢印(↦)の違いに注意してください。
また、a≠a’なのにf(a)=f(a’)であったり、Bのある元bに対してf(a)=bとなるようなaが存在しなくても大丈夫です。
1つの元を入力したら1つの元が出力されるなら写像、と理解しましょう。
この定義でAを定義域、Bを終域と言います。
また、f(A)\(\colon\)={f(a)\(\in\)B:a\(\in\)A}を値域といいます。
例
関数は全て写像です。例えば、f(x)=x²はなにか1つの元(つまり数字)を入力したときに1つの値が出力されるようなものなので写像です。
2変数関数では、2つの変数を両方合わせて1つの元として考えます。(これについては直積の部分でまた詳しく説明します)
しかし、f:R→R,x↦x³/x とすると、これは写像ではありません。0に対しての定義がされてないからです。これは定義域を狭めることで写像になります。
f:R\(\backslash\){0}→R,x↦x³/x は写像になります。
A={a,b,21},B={A,{A},0}として
f:A→Bをa↦{A},b↦A,21↦A と定義するとfは写像になっています。1つの入力に対して1つの出力となっていることが分かります。
単射、全射、全単射
写像がある条件を満たすとき、名前を付けます。定義の下にイメージ図を載せます(汚い絵ですいません)。この定義でイメージ図となることを確認すると理解が深まっていいかと思います。
写像f:A→Bが単射
\(\overset{def}{\Leftrightarrow} [f(a)=f(a’)\Rightarrow a=a’]\)
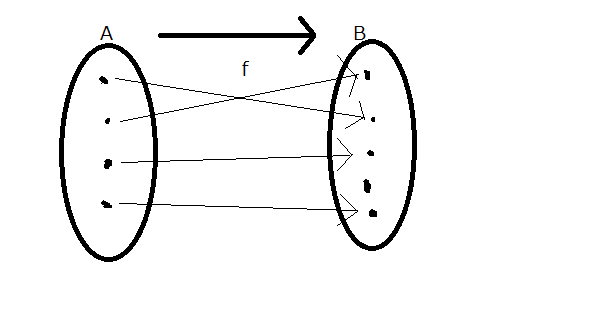
単射のイメージは出力が同じならば入力も同じ、対偶をとって出力が違うなら入力が違う、つまり最初が違ったら行先でも違うということです。
写像f:A→Bが全射
\(\overset{def}{\Leftrightarrow} [^{\forall}b\in B \Rightarrow (\exists a\in A s.t.f^{-1}(b)=a)]\)
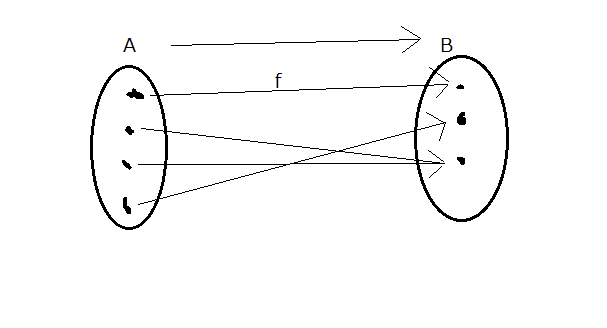
ここで\(f^{-1}\)は写像fの逆像といって、定義は以下です。
\(f^{-1}\)(b):={a\(\in\) A:\(f\)(a)=b}
ここで一般的に逆像は写像ではないことに注意しましょう。例えば、f(x)=x²の逆像は±\(\sqrt{x}\)となり、x≠0なら1つの入力に対して2つの出力があるので写像ではありません。
全射のイメージは値域=終域です。行先全ての和集合が終域になるときを言います。
単射かつ全射な写像を全単射と呼びます。これは俗に一対一対応とも言います。
まとめ
今回は写像、単射、全射、全単射の定義について紹介しました。
イメージがつかめるとあまり難しくはないかと思います。これも論理記号と同じく、定義は覚えるもので覚えた先に言語としての面白味があるものですので頑張って覚えましょう。
今回もお付き合いありがとうございました!次回はもう少し込み入った定義を紹介したいと思います。
質問や挙げてほしいトピック等ありましたら大歓迎です。コメント欄まで書いてもらえると幸いです。


コメント