こんにちは!マシューの数理理論部屋です。
今回も前回に引き続き論理学について書いていこうと思います。
よろしくお願いします。
公理系
今回、そして以後の公理系として次のものを仮定します。
\(^{\forall} A\) \((Aは命題)\)に対して
- \(A\land \lnot A\)は常に偽
- \(A\lor \lnot A\)は常に真
この公理は、
1つ目が\(A\)でありながら\(A\)でないことはない
2つ目が必ず\(A\)または\(A\)でない
という意味ですので、\(A\)という命題は必ず真か偽のどちらか一方のみである、という結論が得られることが分かるかと思います。
この公理について、当たり前と感じる方もいらっしゃるのではないかと思います。
しかし、数学においては仮定をしっかりと把握したうえで議論を進めることが大事なので掘り返すような形ではありますが、上の公理を書きました。勿論、上記のような公理が成り立たないような場合の数学も研究されていますが、今回はそこについては触れないことにします。
対偶
対偶(1)については、高校数学で集合を習った際に触れたのではないでしょうか。
\(A\Rightarrow B\)の対偶は\(\lnot B\Rightarrow \lnot A\) ・・・(1)
これはベン図で説明がされたかと思います。
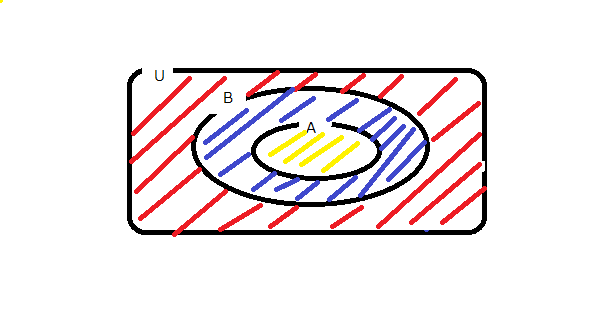
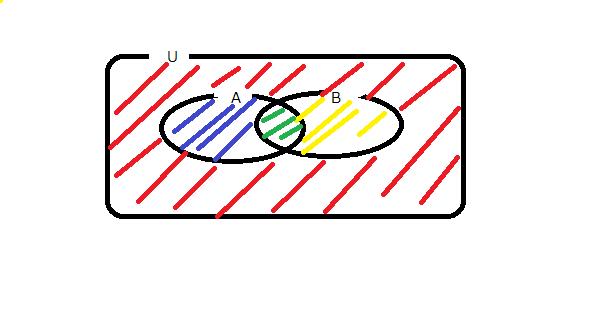
全ての命題をUとして、\(A\Rightarrow B\)が真ならば、一般的に上左図のようなベン図を書くことができます。この時、命題が\(A\)に含まれていれば、\(B\)にも含まれているので\(B^C \subset A^C\)も真だとわかります。
また\(A\Rightarrow B\)が偽ならば、一般的に上右図のようなベン図を書くことができます。この時、\(B^C \subset A^C\)も偽だとわかります。
以上より、\(A\Rightarrow B\)の真偽と\(\lnot B \Rightarrow \lnot A\)の真偽が一致する分かったかと思います。
以下では、この対偶を使って示せる例を書きたいと思います。
背理法
これも高校数学で習ったのではないでしょうか?\(\sqrt{2}\)が有理数でないことを示すために背理法を使う問題などは有名かと思います。
実は私、高校生の時に何故背理法が証明の方法として有効なのか(つまり、背理法で証明できる理由)が分かってませんでした。この背理法は、対偶を使ってすぐに正当性を示すことができます。
背理法は、まず(仮定が真であるという前提のもと)結論が偽であると仮定して(つまり結論の否定を仮定)、矛盾を示すことで[結論が偽である]ことが偽である(つまり結論が真である)ことを示す方法です。
論理式にすると以下のようになります。
\([(A\Rightarrow \lnot B)\Rightarrow (\lnot C \land C)]\Rightarrow (A\Rightarrow B)\)
ここで\(\lnot C \land C\)の部分が上記の公理系に反するので、\((A\Rightarrow \lnot B)\Rightarrow (\lnot C \land C)\)では推論が正しいのに結論が偽ということになります。
このような状況は真偽表により仮定が偽なる状況なので、\(A\Rightarrow \lnot B\)が偽とわかります。
\(A\Rightarrow \lnot B\)が偽ということは、真偽表では\(A\)が真かつ\(\lnot B\)が偽である場合しかないので、\(B\)が真であることが分かります。
以上より、\(A\)が真の時、\(B\)も真になるので、\(A\Rightarrow B\)が真というわけです。
まとめ
今回は公理系を仮定した上で対偶と背理法について説明しました。論理記号の定義も含めて何度でも見返すと論理学としての言語能力が高まり理解が深まるのではないかと思います。
さて、今回の題材のなかで”真偽表”という言葉が出てきました。これは簡単に説明すると\(A\Rightarrow B\)という命題に対して\(A\)が真の時と偽の時、そして\(B\)が真の時と偽の時と4通りの組合わせがありますが、どのようなときに真となって偽となるかということを示した表です。
次回はこの真偽表を構成していくうえで、\(A\Rightarrow B\)を更に見ていきたいと思います。
最後までお付き合いいただきありがとうございました。これからもマシューのD&D部屋をよろしくお願いします。また挙げてほしいトピックや質問等ありましたら大歓迎です。



コメント