こんにちは!マシューの数理理論部屋です。
今回は前回紹介した地球の内部構造を使って実際に地球の慣性モーメントを計算していきます。
地球の慣性モーメントの計算
早速計算にうつりたいと思います。
いきなり内部構造が複雑な地球の慣性モーメントを計算するのではなく、順序を立てて計算していくことにします。既に計算方法を知っている方、読み飛ばして計算結果だけを見たい方は読み飛ばしていただいても大丈夫です。
極座標の体積積分要素
球の慣性モーメントの求め方はいくつかありますが、今回は後での利便性のため、極座標を用いて求めようと思います。
さて、慣性モーメントは式(1)で定義されてました。
\(\displaystyle \int \rho(\overset{\rightarrow}{x})s^2(\overset{\rightarrow}{x})dV\)・・・(1)
この式の意味については前回説明しています。注意点としては、極座標を用いているので回転軸からの距離は\(r\)ではなく\(s\)としています。
ここで\(\int dV\)は極座標のヤコビアンが\(r^2sin\theta \)ですので、
\(\displaystyle \int dV =\displaystyle \int r^2 sin\theta dr d\theta d\phi\)・・・(2)
となります。
積分の計算
次に回転軸からの距離\(s(\overset{\rightarrow}{x})\)について計算します。
これは単純に下図のように考えると\(s(\overset{\rightarrow}{x})=rsin\theta \)だとわかります。
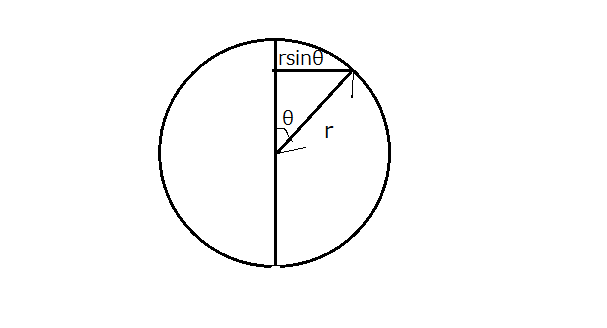
これより、(1)式は(3)式のように書き換えることができます。
\(\displaystyle \int \rho(\overset{\rightarrow}{x})s^2(\overset{\rightarrow}{x})dV=\displaystyle \int \rho r^4 sin^3\theta drd\theta d\phi \)・・・(3)
実際にこれを計算していきます。後での準備のために\(r\)積分はa≦\(r\)≦bで積分します。
\(I=\displaystyle \int \rho r^4 sin^3\theta drd\theta d\phi \\=\rho (\displaystyle \int_a^b r^4 dr)(\displaystyle \int_0^{\pi}sin^3 \theta d\theta)(\displaystyle \int_0^{2\pi}d\phi)\\=\rho \displaystyle \frac{b^5-a^5}{5}(\displaystyle \int_0^{\pi}sin\theta d\theta -\displaystyle \int_0^{\pi} cos^2 \theta sin\theta d\theta)2\pi \\=\displaystyle \frac{2\pi \rho (b^5-a^5)}{5}([-cos\theta]_0^{\pi} -\displaystyle \int_{-1}^1 t^2 dt)\\=\displaystyle \frac{2\pi \rho (b^5-a^5}{5}(2-\displaystyle \frac{2}{3})=\displaystyle \frac{8\pi \rho (b^5-a^5)}{15}\)・・・(4)
さて、これで半径が\(a\)から\(b\)までの球殻(半径\(b\)の球から半径\(a\)の球をとったもの)の慣性モーメントが分かりました。
地球の各層の慣性モーメント
では実際に地球の各層の慣性モーメントを計算していきます。これは式(4)の最右辺に層の情報\(a,b,\rho \)を代入していけば終わりです。各層の物理量(と状態)を再掲します。
| 名前 | 厚さ | 密度 | 状態 |
| 地殻 | \(14.7km\) | \(2900kg/m^3\) | 固体 |
| マントル | \(2900km\) | \(4000kg/m^3\) | 固体 |
| 外核 | \(2200km\) | \(12600kg/m^3\) | 液体 |
| 内核 | \(1300km\) | \(13800kg/m^3\) | 固体 |
地球は半径6414.7kmの完全な球として計算していきます。長さの単位を合わせると下表のようになります。
| 名前 | 厚さ | 密度 | 状態 |
| 地殻 | \(14.7km\) | \(2.9×10^{12}kg/km^3\) | 固体 |
| マントル | \(2900km\) | \(4×10^{12}kg/km^3\) | 固体 |
| 外核 | \(2200km\) | \(1.26×10^{13}kg/km^3\) | 液体 |
| 内核 | \(1300km\) | \(1.38×10^{13}kg/km^3\) | 固体 |
\(I_{地殻}=\displaystyle \frac{8\pi 2.9×10^{12} (6414.7^5-6400^5)}{15}=6.02×10^{29}[kg・km^2]\)
\(I_{マントル}=\displaystyle \frac{8\pi 4×10^{12} (6400^5-3500^5)}{15}=6.84×10^{31}[kg・km^2]\)
\(I_{外核}=\displaystyle \frac{8\pi 1.26 ×10^{13}(3500^5-1300^5)}{15}=1.10×10^{31}[kg・km^2]\)
\(I_{内核}=\displaystyle \frac{8\pi 1.38×10^{13}(1300^5-0^5)}{15}=6.22×10^{31}[kg・km^2]\)
地球全体の慣性モーメント
各層の慣性モーメントが求まりました。あとはこれらを足していけば地球全体の慣性モーメントが求まります。
まず何故単純に足し合わせると慣性モーメントとして成立するかを説明します。以下では2つの物体があった時に全体の慣性モーメントが2つの慣性モーメントの足し合わせであることを示していますが、2つの足し合わせができれば以降3つ、4つ・・・は同じことなので足し合わせで求めることができるとわかります。
同じ軸を回転軸に持つ2つの物体A,Bがあるとします(AとBは共通部分を持たないと仮定、つまりAとBが溶け合うことがないとします)。A,Bの慣性モーメントはそれぞれ\(I_A,I_B\)とします。これはそれぞれの密度関数\(\rho_{A}(\overset{\rightarrow}{x}),\rho_{B}(\overset{\rightarrow}{x})\)と軸からの距離関数\(r_{A}(\overset{\rightarrow}{x}),r_{B}(\overset{\rightarrow}{x})\)を仮定して\(I_A=\int \rho_{A}(\overset{\rightarrow}{x}) r^2_{A}(\overset{\rightarrow}{x})dV, I_B=\int \rho_{B}(\overset{\rightarrow}{x}) r^2_{B}(\overset{\rightarrow}{x})dV\)であるという意味です。
ここでCをAとBの全体を1つの物質としてみたものとします。Cの各点上での密度関数と軸上の距離関数は、Aに含まれている点であればAのものに、Bに含まれている点であればBのものに依存するので慣性モーメント\(I_C\)は積分の中身を分けて
\(I_C = \displaystyle \int_A \rho_A(\overset{\rightarrow}{x}) r^2(\overset{\rightarrow}{x})dV + \displaystyle \int_B \rho_B (\overset{\rightarrow}{x}) r^2 (\overset{\rightarrow}{x}) dV \\ = I_A + I_B\)
積分記号\(\int dV\)の添え字として書いてあるAやBはそれぞれAについての体積分、Bについての体積分という意味です。
本来はもう少し厳密に示す必要があるのですが、それはルベーグ積分の範囲となるので今回は省略してます。
蛇足ですが、物理学においてはあまり数学的な厳密性は求めてない印象です。使えるから、もしくは計算してみて実験と合っていたから、程度で数学を使ってしまう場合もあります。物理学の教科書に証明と書いてあるのに実は証明にはなっていないこともあるので注意しましょう。
話が長くなりましたが、結局地球全体の慣性モーメントは
\(I_{地球}=I_{地殻}+I_{マントル}+I_{外核}+I_{内核}=8×10^{31}[kg・km^2]\)
となります。ほとんどがマントルの慣性モーメントだとわかりますね。
考察
上では内部構造を用いて地球の慣性モーメントを求めました。慣性モーメントは回し易さを表すものなので、他の天体との重力作用で求めることができます。
地球内部物理学 – Wikipediaによると慣性モーメントは
\(I_{地球}=0.33Ma^2=8.11×10^{31}[kg・km^2]\)
です。上での計算結果と比べると1.4%程の差はあるもののかなりいい値で出たようです。私自身10%程度の範囲に入ればいいかなと思っていたのでびっくりしました。
一応、この1.4%の誤差の理由について羅列したいと思います。
- 各層の深さや密度が正確でない
- 各層ごとの密度が一定ではない
- 地球も各層も完全な球ではない
- 外核が液体なので剛体として扱うことができない
おそらくこれらの要因の誤差が打ち消しあっているから1.4%程度の誤差に収まったのかと思います。
まとめ
今回は地球の内部構造を用いて慣性モーメントを求めました。結果は1.4%の精度となり、満足いく値だと思います。
次回はこの慣性モーメントを使って地球の(自転の)角運動量とコロニーの(公転)の角運動量を計算していきます。
今回は量も多めで大変だったかと思います。最後まで読んでくれた方、ありがとうございました。次回もよろしくお願いします。


コメント